6. Property-based Testing and Test Oracles#
6.1. Learning outcomes of this chapter#
At the end of this chapter, you should be able to:
Define the terms “property-based testing” and “test oracle”.
Contrast the different types of test oracle.
Choose the correct type of test oracle for a given problem.
Design an oracle for a program from a specification.
Apply property-based testing to test a non-trivial piece of software
Describe the strengths and weaknesses of property-based testing
6.2. Chapter Introduction#
In this chapter, we will discuss test oracles and property-based testing. Recall from Section Black-Box and White-Box Testing that a test case consist of three elements:
a test input or sequence of test inputs;
an expected output or sequence of expected outputs; and
the testing environment.
The normal procedure for executing a test case is to execute the program using the inputs in the test case, record the results, and then to determine if the outputs obtained are failures or not.
Who or what determines if the results produced by a program are failures? One way is for a human tester to look at the input and manually calculate that they believe the output should be. In this case the human tester is playing the role of a test oracle.
A test oracle is someone or something that determines whether or not the program has passed or failed the test case. Of course, it can be another program that returns a “yes” if the actual results are not failures and “no” if they are.
Definition
A test oracle is:
a program;
a process;
a body of data;
that determines if actual output from a program has failed or not.
Ideally an oracle should be automated (no human intervention at runtime) because then we can execute a larger volume of test cases and gain greater coverage of the program, but this is often non-trivial in practice.
However, what we can do is to define properties that should hold in our program for specific inputs. For example, if we test a sorting algorithm, one property that should hold is that, for each element \(i\) in the list, the element at \(i+1\) should be greater than or equal to this: for all \(i \in [0..length(list)-1], list[i] \leq list[i+1]\).
6.3. Active and Passive Test Oracles#
An automated oracle can be placed into one of two categories:
Active oracle: A program that, given an input for a program-under-test, can generate the expected output of that input.
Passive oracle: A program that, given an input for a program-under-test, and the actual output produced by that program-under-test, verifies whether the actual output is correct.
Passive oracles are generally preferred. This is for two main reasons.
Firstly, passive oracles are typically easier to implement than active oracles. For example, consider testing a program that sorts a list of numbers. It is considerably easier to check that an output produced by the is a sorted list, than it is to sort this list. This not only saves the tester some time, but also means that there is less chance of introducing a fault into the oracle itself. If the active oracle is required to simulate the entire program-under-test, it may be as difficult to implement, and therefore, is just as likely to contain faults of its own.
The second reason that passive oracles are preferred is because they can handle non-determinism. Recall from Section Programs, that a program is non-deterministic if it can return more than one output for a single input. If an active oracle is used, there is a good chance that the output produced by the will be different to the output produced by the active oracle. However, if we use a passive oracle, which simply checks whether the output is correct, then non-determinism is not an issue.
6.4. Types of Test Oracle#
In general, to design a test oracle, there are several types of oracle that can be produce, which are categorised by the way their are derived, or the way they run.
6.4.1. Formal, executable specifications#
Formal specifications written in a tight mathematical notation are better for selecting and creating testing oracles than informal specification written in a natural language. They can be used as active oracles by generating expected output using a simulation tool, or as passive oracle, by proving that the specification is satisfied by the input and the actual output. These are unlikely in practice, and are mostly reserved by high integrity applications such as safety-, security-, or mission-critical systems.
6.4.2. Solved examples#
Solved examples are developed by hand, or the results from a test input can be obtained from texts and other reference works. This is especially useful for complex domains, in which deriving the expected output automatically requires a process as complicated as the program itself, and deriving it manually requires expertise in a specific area that a test engineer is unlikely to have.
Data in the form of tables, documents, graphs or other recorded results are a good form of testing oracle. The test input and actual results can be looked up in a table or data-base to see if they are correct or not.
These types of oracles have the disadvantage that the inputs chosen are restricted to the examples that we have access to. Despite this, they are common due to their abundance in many fields.
6.4.3. Metamorphic oracles#
In some cases, we can use certain metamorphic properties between tests to check each other. By ‘metamorphic’, we mean that, given two different inputs that are related by some property \(p\), if we run them both through our program, their outputs will be related by some other property \(q\). The metamorphic relation is the relationship between \(p\) and \(q\).
For example, if we want to test a function that sorts a list of numbers, then we can make use of the fact that, given a list, any permutation of that list will result in the same output of the sort function (assuming a non-stable sort).
To do metamorphic testing, we generate an input for a program, execute this input, and then generate another input whose output will be related to the first.
Formally, metamorphic testing follows the following pattern to test a function \(f\):
Given input \(i\), generate another input \(j\), such that property \(p(i, j)\) holds between \(i\) and \(j\).
Obtain outputs \(o_i = f(i)\) and \(o_j = f(j)\).
Check whether \(q(o_i, o_j)\) holds between \(o_i\) and \(o_j\), raising an error if it fails.
Example – Metamorphic testing for a \(sort\) function
In the sorting example, we can generate a test input as a list of numbers, and then randomly permute the elements of the list to get a new list. Then, we execute both tests on the sort function, and compare their output. If their output is different, then we have produced a failure. A test for this could be written as follows:
void testSortMetamorphic(int [] list)
{
int [] permutatedList = permutate(list);
output1 = sort(list);
output2 = sort(permutatedList);
assertEquals(output1, output2);
}
In this case, the property \(p(i,j)\) is that the list and permutatedList have the same items, but in a different order. The property \(q(o_i,o_j)\) is the equality relation: output1 and output2 have the same elements in the same order.
Example — Metamorphic testing for a \(shortestPath\) function
Another example is a program for finding the shortest path between two nodes on a graph for a GPS-enabled device. If the algorithm finds the shortest path between the start point and the destination, a complete oracle would need to check that this is indeed the shortest path. However, to check this fully, our oracle would have to re-calculate the shortest path as well, which would likely be as complicated as the original algorithm, and therefore just as prone to faults.
A metamorphic testing approach would be as follows. We can select any two nodes on the graph and run the program, returning a path \(P_1\). To check if this path is correct, we can select any two nodes on the path \(P_1\) and run the shortest path program on those two nodes. This will return a new path \(P_2\). Path \(P_2\) should be a sub-path of \(P_1\).
For example, consider the following driving path from the Melbourne Connect building at the University of Melbourne, to Edinburgh Gardens in Fitzroy:
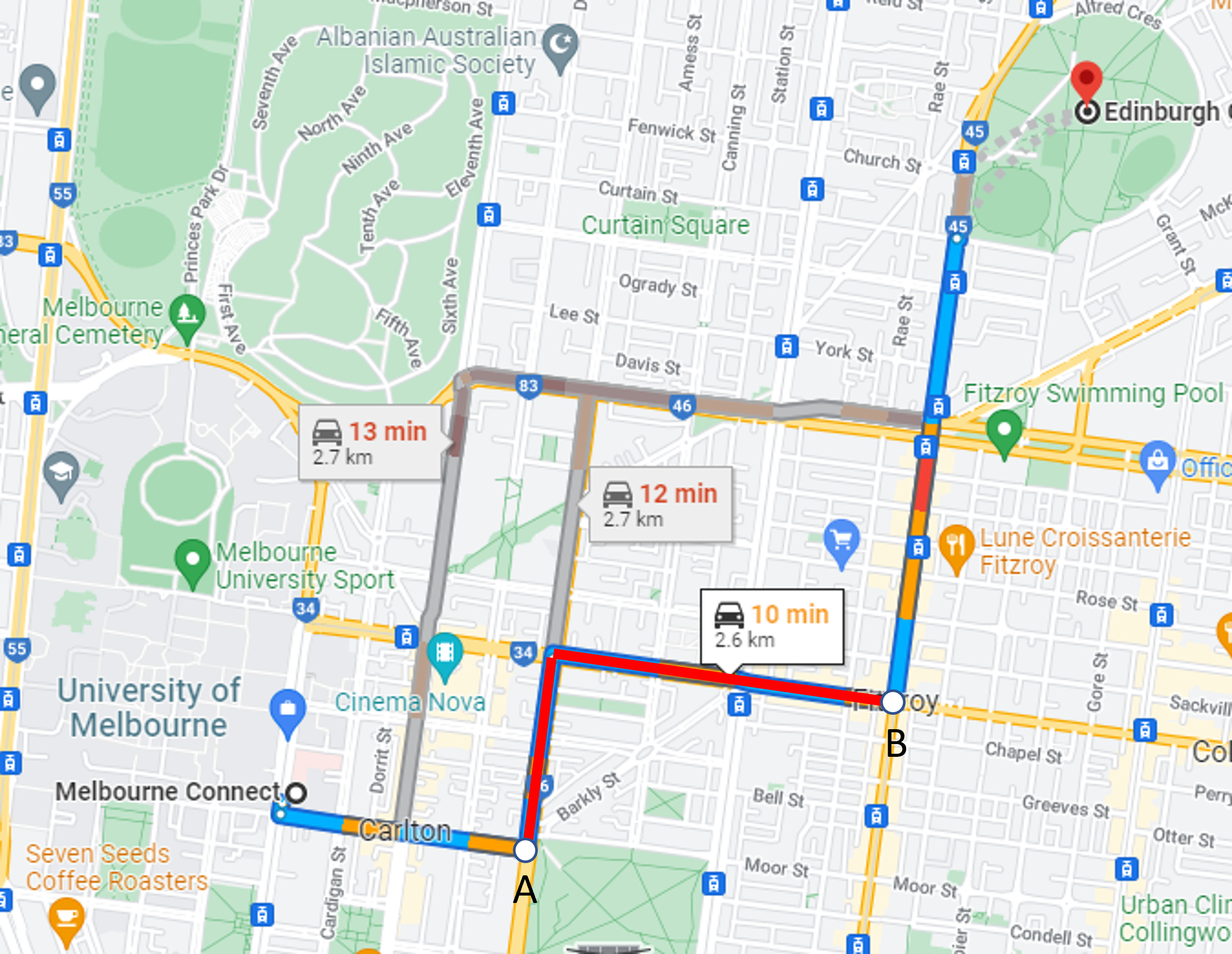
The blue path represents \(P_1\), the output of the algorithm on the two original points, while the red path represents \(P_2\), the output of the algorithm for two random points \(A\) and \(A\) along that path. Then, \(P_2\) should be a sub-path of the original path \(P_1\).
An implementation of such an approach would be as follows:
void testShortestPathMetamorphic(Graph graph)
{
Node node1 = selectRandomNode(graph);
Node node2 = selectRandomNode(graph);
Path path1 = shortestPath(node1, node2, graph);
Node node3 = selectRandomNode(path);
Node node4 = selectRandomNode(path);
Path path2 = shortestPath(node3, node4, graph);
assertTrue(isSubPath(path2, path1);
}
Here, the property \(p(i,j)\) is that the node3 and node4 are two nodes on the shortest path of graph. The property \(q(o_i,o_j)\) is the sub-path relation: path2 is a sub-path of path2.
In these tests, we can loop around the code in the body of testSortMetamorphic and testShortestPathMetamorphic hundreds or thousands of times to run multiple tests on the same property.
The existence of metamorphic properties for programs is surprisingly common, and metamorphic oracles have been used to test many numerical programs, but also many applications in non-numerical domains as well, including bioinformatics, search engines, machine learning, medical imaging, and web services.
6.4.4. Alternate implementations#
An alternate implementation of a program, which can be executed to get the expected output. This is not ideal because experience has shown that faults in different implementations of the same specification tend to be located on the same inputs. Therefore, an alternate implementation is likely to have the same faults as the program-under-test, and some faults would not be detected via testing as a result.
One approach that has shown to be useful is to provide a partial, simplified version of the implementation, which does not implement the full behaviour of the program-under-test, and does not consider efficiency or memory.
Example — Partial oracle for a \(sort\) algorithm
If we have an efficient sorting algorithm, then we can restrict the oracle (the alternative implementation) to only working on lists of integers whose values, when sorted, form a complete integer sequence; e.g., \(10, 11, 12, 13, 14, 15\). To perform the sort, the oracle needs to know the lowest and highest element of the list, and then return a list with the lowest element at the first index, the highest element at the last, and the corresponding elements in between. This is partial, and perhaps not efficient, but it results in a list that is a sorted version of the inputs, and is less likely to contain a fault than the original sorting algorithm due to its reduced complexity.
/**
* @assumption: elements in list form a complete integer sequence,
* not necessarily in order
* /
void testSort(int minimum, int maximum)
{
int [] expectedOutput = new int [list.length];
for (int i = minimum; i < list.length; i++) {
expectedOutput[i] = minimum + i;
}
int [] input = permutate(expectedOutput);
int [] actualOutput = sort(list);
assertEquals(actualOutput, expectedOutput);
}
Such an approach restricts the test inputs that can be used, but is often sufficient to find many faults in a system.
6.4.5. Heuristic oracles#
Another type of widely-used oracle are heuristic oracles. These are oracles that provide approximate results for inputs, and tests that “fail” must be scrutinised closely to check whether they are a true or false positive.
The trick with heuristic oracles is to find patterns in complex programs — that is, patterns between the inputs and outputs — and exploit them. For example, a simple heuristic of databases is that, when a new record is inserted into a table, the number of records in that table should increase by 1. We can run thousands of tests inserting single records, and checking that the number of rows in table increases by 1. This is not complete though, because we are not checking that the contents of the row are accurate.
Example — Testing a GPS path search algorithm
Let’s return to the GPS shortest path algorithm example from earlier. We can use the heuristic that the shortest path cannot possibly be shorter than a straight line between the two points. For example, consider again the driving path from the Melbourne Connect building at the University of Melbourne, to Edinburgh Gardens in Fitzroy:
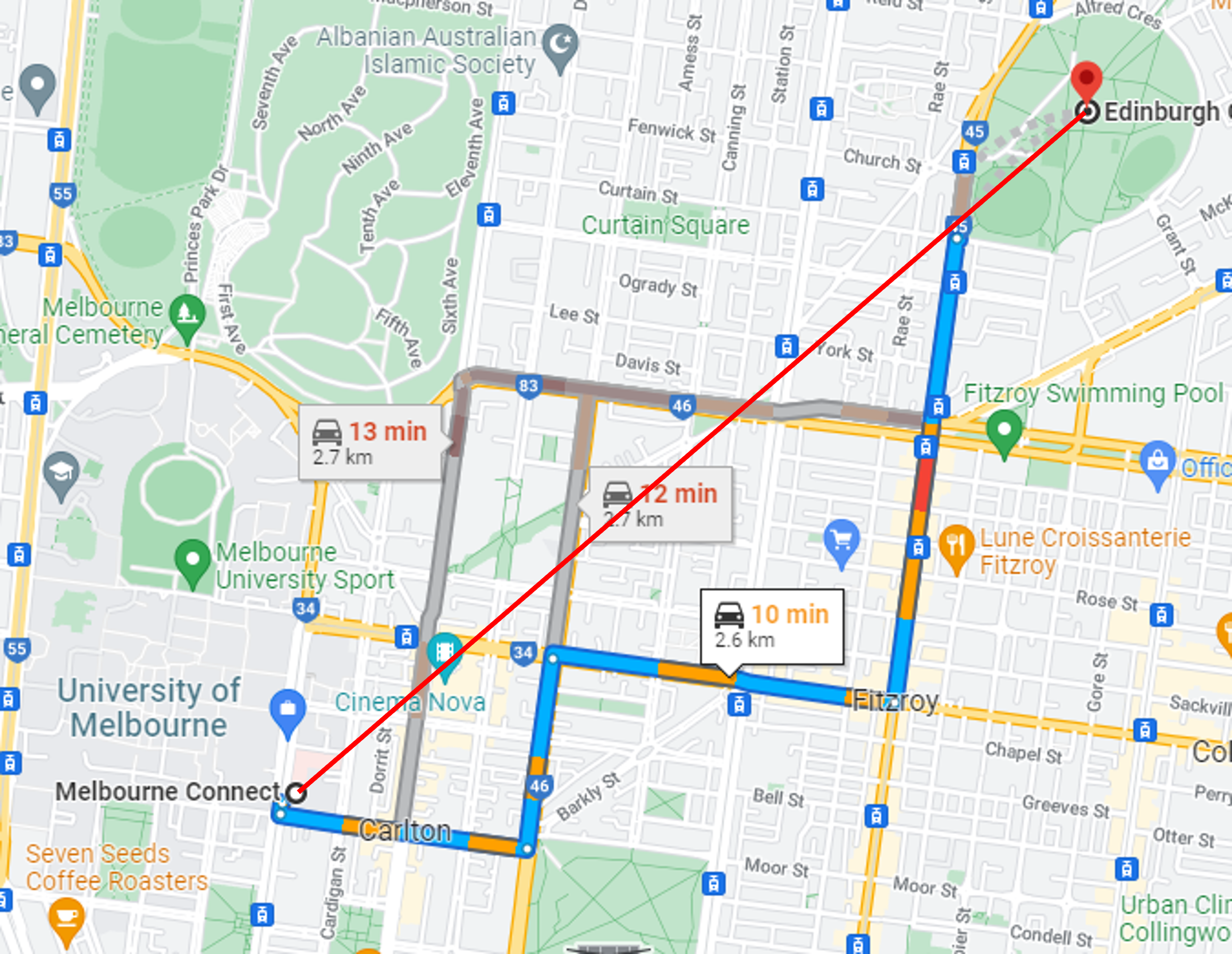
The red line represents the shortest straight line (“as the crow flies”) between the two points. This red line cannot be longer than the driving path between the two points. Any path that is reported shorter than the red line must indicate a fault.
This is useful because the calculation of the shortest line is quite different to the calculation of the shortest path: it ignores the roads and is a simple mathematical calculation given the coordinates of the two points.
This heuristic is sound, but not complete. By ‘sound’, we mean that, if the heuristic raises an error, we know that we have a failure. By ‘complete’, we mean that, if there is a failure, the heuristic will raise an error. This oracle is not complete because it is possible that faults in the software will lead to incorrect paths that are longer than the red line. However, it may still be useful for finding some faults.
So, this heuristic, while correct, may not find many faults if the algorithm is pretty good, but not great. We can tighten up the heurstic to say that the shortest path should be within, e.g. 1.5 times the distance of the straight line between the two points. Anything outside of this could signal a fault. This is clearly not complete, as before, however, it is also not sound: the distance between two points may be small, while the shortest path via a road network may have to go around a body of water, such as the following route from Sorrento beach to Queenscliff:
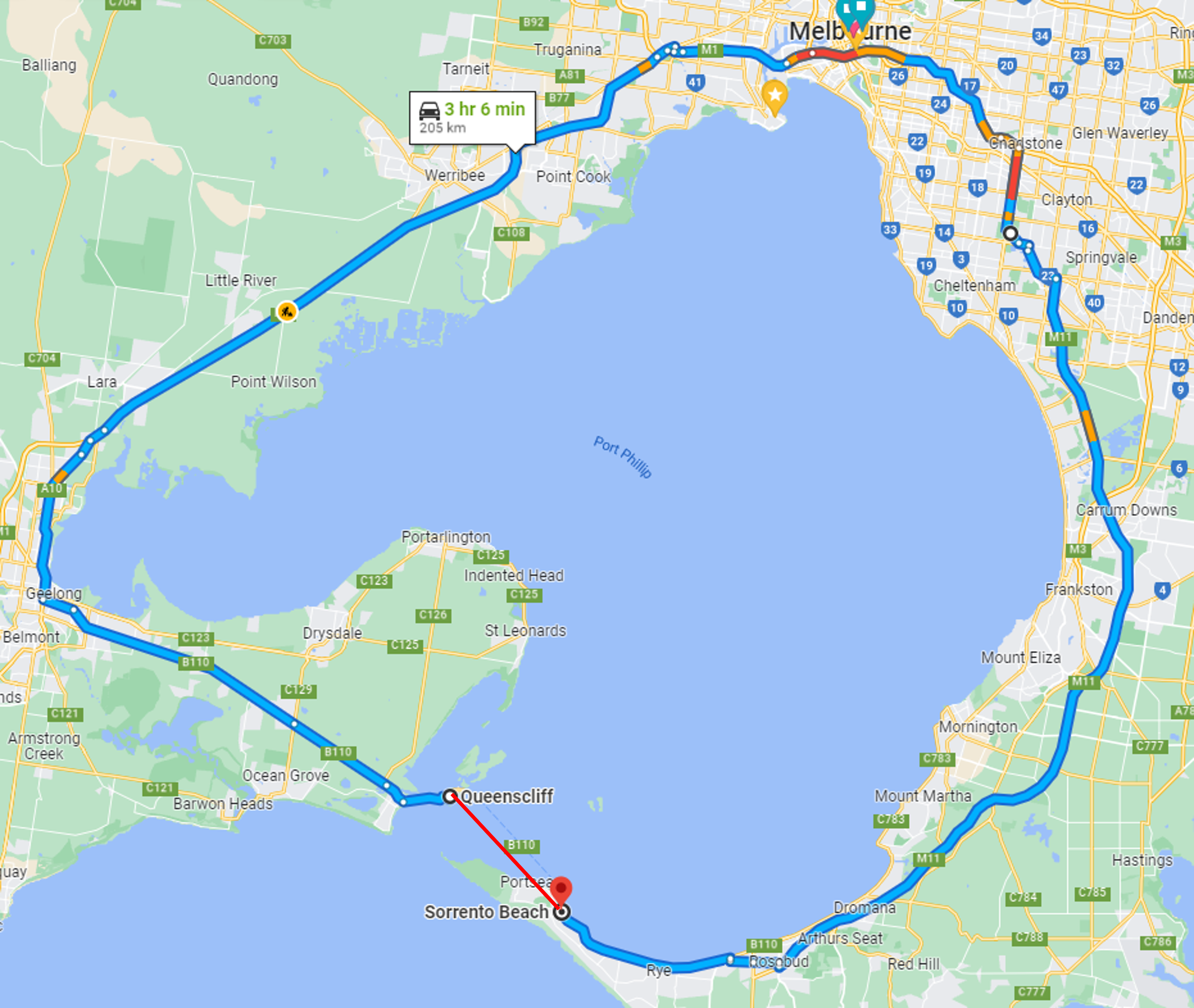
Here, the red line is much shorter than the recommended path, but the recommended path is the best line (unless you take the ferry!).
In reality, most oracles are heuristic, in that none of them really replicates the expected behaviour of the corresponding program. However, we use the term heuristic oracle to refer to oracles that are designed based on some heuristics that are not complete, maybe not sound, but test some properties of software under test.
6.4.6. The Golden Program!#
The ultimate source for a testing oracle but rare in practice. The golden program is an executable specification, a previous versions of the same program, or test in parallel with a trusted system that delivers the same functionality.
Still, the golden program is not a pipedream. In industry, it is not uncommon to use the previous release of a piece of software as a test oracle.
6.4.7. Oracle derivation#
In these notes, we will not consider how to derive oracles. Current industry practice leaves much of the test case generation, including the oracle, up to human testers, who typically derive the oracles by looking at the specification and design of the artifact that are testing. In many unfortunate cases, the tester is left to guess what the behaviour of the software should be.
State-of-the-art testing includes model-based testing, which is used to automate both input and oracle generation. Using model-based testing, rather than the test engineer deriving test cases, he/she derives a model of the expected behaviour of the program-under-test, using some formal, executable language. From this model, test inputs are generated automatically (using the types of criteria that we discuss in these notes), and the expected outputs for those inputs are calculated by simulating the model. This can be seen as a cross between the first and last types of oracle. The model can be seen as an abstract alternative of the implementation, which is both formal and executable. However, unlike other alternate implementations, the higher level of abstract means that the likelihood of faults being located on the same inputs is reduced. Empirical evidence demonstrates that model-based testing is, in general, no more expensive than manual test case generation, and in many cases, is significantly more efficient, and is as successful for locating faults.
6.5. Property-based testing#
Once we have an oracle for a program, even a partial oracle, we can use property-based testing to execute a large volume of tests on our program.
A weakness of functional testing using techniques such as equivalence partitioning is that it is time consuming to find good tests; and further, we aim to select only a small number. This is not so good for testing the robustness of software.
Property-based testing combines the idea of (usually passive) test oracles with techniques such as random testing to run a large amount of test inputs, and check their output against certain properties.
6.5.1. Defining property-based templates#
The general template of a property-based test is as follows:
for all (x, y, z, ...)
such that condition(x, y, z) holds
property(x, y, z, ..., f(x, y, z, ...)) is true.
where x, y, z, ... are input variables, and f is a function that we are testing. condition is a predicate that returns true if some property is true for x, y, z, ..., while property is a test oracle that returns true if the some property holds true between the inputs in x, y, z, ... and the output of the program f(x, y, z, ...).
We can then write a test driver that generates random inputs for our variables x, y, z, etc., filters out those that do not hold for the condition (alternatively we can generate inputs that only hold for the condition), run those tests on f, observe the output, and then check that the property holds.
Metamorphic testing is one form of property-based testing. In metamorphic testing, condition is the relation, \(p(i,j)\), on the input, and property is the relation, \(q(o_i, o_j)\), on the outputs.
However, we can test properties other than metamorphic properties.
Example
Consider the example of the triangle program in the Input partitioning. What are some properties that hold for triangles?
First, if any side is negative, then the triangle is invalid. We can generate random side lengths between [1, 100] for two sides and [-100, 0] for others, and then test this a number of times:
@Test
void testNegativeSides()
{
Random r = new java.util.Random();
for (int i = 0; i < iterations; i++) {
int x = r.nextInt(100);
int y = r.nextInt(100);
int z = -r.nextInt(100);
assertEquals(categoriseTriangle(x, y, z), Triangle.invalid);
assertEquals(categoriseTriangle(z, x, y), Triangle.invalid);
assertEquals(categoriseTriangle(y, z, x), Triangle.invalid);
}
}
In the code above, we randomly generate only inputs such that one side of the triangle is non-positive, rather than generating any set of random numbers and then filtering based on the condition.
A second property is that one size cannot be larger than the sum of the other two sizes. Again, we can generate random inputs that violate this:
@Test
void testLongSide()
{
Random r = new java.util.Random();
for (int i = 0; i < iterations; i++) {
int x = r.nextInt(100) + 1
int y = r.nextInt(100) + 1;
int z = r.nextInt(100) + x + y + 1;
assertEquals(categoriseTriangle(x, y, z), Triangle.invalid);
assertEquals(categoriseTriangle(z, x, y), Triangle.invalid);
assertEquals(categoriseTriangle(y, z, x), Triangle.invalid);
}
}
We can implement similar checks for equivalence and isosceles classes:
@Test
void testEquilateral()
{
Random r = new java.util.Random();
for (int i = 0; i < iterations; i++) {
int x = r.nextInt(100)
assertEquals(categoriseTriangle(x, x, x), Triangle.equilateral);
}
}
@Test
void testIsosceles()
{
Random r = new java.util.Random();
for (int i = 0; i < iterations; i++) {
int x = r.nextInt(100) + 1;
int y = r.nextInt(100) + 1;
//Filter out sides where x = y = z
if (x != y) {
assertEquals(categoriseTriangle(x, x, y), Triangle.isosceles);
assertEquals(categoriseTriangle(x, y, x), Triangle.isosceles);
assertEquals(categoriseTriangle(y, x, x), Triangle.isosceles);
}
}
}
@Test
void testScalene()
{
Random r = new java.util.Random();
for (int i = 0; i < iterations; i++) {
int x = r.nextInt(100) + 1;
int y = r.nextInt(100) + 1;
int z = r.nextInt(x + y); //x + y < z
//Filter out sides where x = y, y = z, or x = z
if (x != y && x != z && y != z) {
assertEquals(categoriseTriangle(x, y, z), Triangle.scalene);
assertEquals(categoriseTriangle(x, y, z), Triangle.scalene);
assertEquals(categoriseTriangle(x, y, z), Triangle.scalene);
}
}
}
In testIsosceles and testScalene, we generate some random side lengths, and then the branches if (x != y) and if (x != y != z) are the conditions that filter out inputs that do not hold for the property. We could instead have represented this explicitly as a property; for example, in testIsosceles, we could state:
assertTrue(x != y, categoriseTriangle(x, x, y) == Triangle.isosceles);
Either of these approaches is valid.
What we can see with the above examples is the pattern of: (1) generating random inputs; (2) such that a condition holds; and (3) checking whether a property holds on those inputs.
6.5.2. Tool support#
A better way to implement property-based testing, rather than doing it by hand, is to use tools designed specifically for the task.
Hypothesis is a property-based testing framework for Python.
jqwik is a property-based testing framework for Java.
Both frameworks help to generate random data, filter out inputs according to the condition, and to specify properties. For example, we could implement the testIsosceles in jqwik as follows:
@Property
boolean isosceles(@Forall("xNotEqualToY") Arbitrary<Tuple.Tuple2<Integer, Integer>> pair)
{
int x = pair.get1();
int y = pair.get2()
return Triangle.categoriseTriangle(x, x, y) == Triangle.isosceles;
}
@Provide
Arbitrary<Tuple2<Integer, Integer>> xNotEqualToY()
{
return Arbitraries.integers().between(1, 100).tuple2.filter(i -> i.get1() != i.get2());
}
This implementation looks a bit complex at first, and indeed, these tools have a short but steep learning curve. In summary, isosceles is the property that we want to test, which is that the triangle x, x, y should be classified as an isosceles triangle, but only if x != y. It should hold for all Integer pairs such that the condition xNotEqualToY holds. This is specified in the parameter declaration @Forall("xNotEqualToY") .... The condition “xNotEqualToY” is defined by the method xNotEqualToY with the @Provide keyword. Arbitraries is a utility class provided by jqwik. In this instance, we generate random pairs of integers between 1 and 100 such the two elements in the pair are not equal, specified using filter(i -> i.get1() != i.get2()). The operator -> can be read as “such that”.
So, this implements the property defined by testIsosceles above, but handles the random test generation. Tools like jqwik also do more than random testing. For example, if they find an example that does not hold, they try to search for a simpler, smaller example that still violates the property. Because this is smaller and simpler, it can make debugging easier.
6.5.3. Strengths and weaknesses of property-based testing#
Compared to example-based functional testing techniques such as input partitioning and control-flow testing, property-based testing has the following strengths:
It can generate a large volume of tests with minimal human oversight and cost.
It encourages us to make our assumptions explicit by defining properties.
It can find things that a human tester does not think of.
But, it also has limitations:
The coverage of the input domain is not systematic, so it is unlikely to test edges cases like boundary values unless explicitly told to, and is unlikely to achieve good coverage of the software unless specifically guided. See the section on random testing for a more detailed discussion with examples.
It only tests the properties that it is given, which are (usually) partial properties. While specifying test oracle that are complete is possible, it is uncommon.
As such, the conclusion is that property-based testing and example-based testing complement each other, so they should be used together; rather than relying on just one technique.
